Los sistemas de numeración son la base de cómo representamos cantidades en diferentes contextos. Aunque estamos acostumbrados al sistema decimal en nuestra vida diaria, en informática y electrónica son fundamentales otros sistemas como el binario, octal y hexadecimal. Vamos a explorar estos sistemas y cómo convertir entre ellos de manera sencilla.

¿Qué es un sistema de numeración?

Un sistema de numeración es un conjunto de símbolos y reglas que nos permiten representar cantidades. Cada sistema tiene una base, que indica cuántos símbolos diferentes utiliza el sistema.

Los sistemas más utilizados:

• Base 2 (Binario): Utiliza solo 0 y 1
• Base 8 (Octal): Utiliza dígitos del 0 al 7
• Base 10 (Decimal): Utiliza dígitos del 0 al 9
• Base 16 (Hexadecimal): Utiliza dígitos del 0 al 9 y letras A-F (donde A=10, B=11, C=12, D=13, E=14, F=15)

Sistema Decimal (Base 10)

Es nuestro sistema habitual donde cada posición representa una potencia de 10:

Mostrar imagen

Por ejemplo, el número 647 en decimal significa:

• 6×10² + 4×10¹ + 7×10⁰
• 6×100 + 4×10 + 7×1
• 600 + 40 + 7 = 647

Otro ejemplo: 3479,52 = 3×10³ + 4×10² + 7×10¹ + 9×10⁰ + 5×10⁻¹ + 2×10⁻² = 3000 + 400 + 70 + 9 + 0,5 + 0,02

Sistema Binario (Base 2)

Es el sistema fundamental en informática. Cada posición representa una potencia de 2:

Mostrar imagen

Las potencias de 2 son: 1 – 2 – 4 – 8 – 16 – 32 – 64 – 128 – 256 – 512 – 1024…

Por ejemplo, el número binario 1001101 equivale a:

• 1×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 1×2² + 0×2¹ + 1×2⁰
• 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77 en decimal

Sistema Octal (Base 8)

Cada posición representa una potencia de 8:

Por ejemplo, el número octal 423 equivale a:

• 4×8² + 2×8¹ + 3×8⁰
• 4×64 + 2×8 + 3×1
• 256 + 16 + 3 = 275 en decimal

Sistema Hexadecimal (Base 16)

Cada posición representa una potencia de 16:

Por ejemplo, el número hexadecimal 423 equivale a:

• 4×16² + 2×16¹ + 3×16⁰
• 4×256 + 2×16 + 3×1
• 1024 + 32 + 3 = 1059 en decimal

Conversiones entre sistemas

Decimal a otros sistemas

Para convertir de decimal a otro sistema (binario, octal, hexadecimal):

1. Dividir el número decimal entre la base del sistema destino
2. Anotar el resto
3. Continuar dividiendo el cociente entre la base
4. Repetir hasta que el cociente sea 0
5. Leer los restos de abajo hacia arriba

Ejemplo: Decimal a Binario (26)

26 ÷ 2 = 13 (resto 0)
13 ÷ 2 = 6  (resto 1)
6 ÷ 2 = 3   (resto 0)
3 ÷ 2 = 1   (resto 1)
1 ÷ 2 = 0   (resto 1)

Resultado: 26 en decimal = 11010 en binario

Decimal a Binario con parte decimal

Para la parte decimal:

1. Multiplicar la parte decimal por 2
2. Tomar la parte entera como dígito binario
3. Seguir multiplicando la parte decimal resultante por 2
4. Repetir hasta obtener 0 como parte decimal o alcanzar precisión deseada

Ejemplo: 77,1875 en decimal a binario

Parte entera (77):

77 ÷ 2 = 38 (resto 1)
38 ÷ 2 = 19 (resto 0)
19 ÷ 2 = 9  (resto 1)
9 ÷ 2 = 4   (resto 1)
4 ÷ 2 = 2   (resto 0)
2 ÷ 2 = 1   (resto 0)
1 ÷ 2 = 0   (resto 1)

77 en decimal = 1001101 en binario

Parte decimal (0,1875):

0,1875 × 2 = 0,375  → 0
0,375 × 2 = 0,75    → 0
0,75 × 2 = 1,5      → 1
0,5 × 2 = 1,0       → 1

0,1875 en decimal = 0,0011 en binario

Por tanto, 77,1875 en decimal = 1001101,0011 en binario

Binario a Decimal

Para convertir de binario a decimal, multiplicamos cada dígito por su posición (potencia de 2) y sumamos:

Ejemplo: 1001101 → 1×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Conversiones entre binario, octal y hexadecimal

La belleza de estos sistemas es que existe una relación directa entre ellos:

• 1 dígito hexadecimal = 4 dígitos binarios
• 1 dígito octal = 3 dígitos binarios

Guía Visual de Sistemas de Numeración

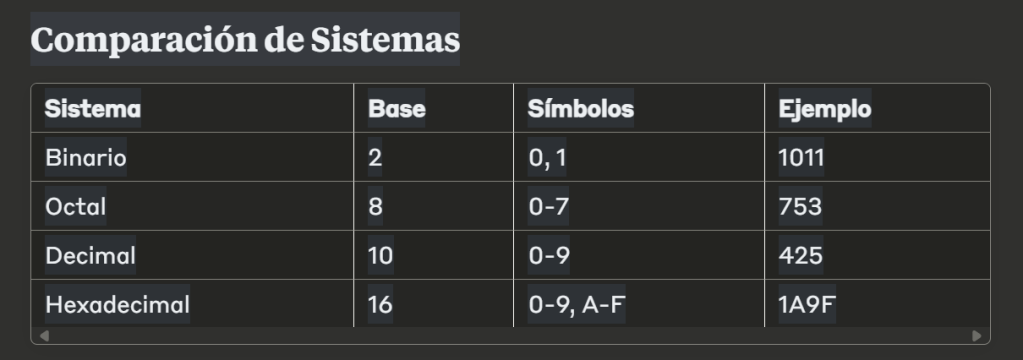
Relación entre sistemas

Ejemplos de conversiones paso a paso

Ejemplo 1: Decimal (77,1875) a Binario

Parte entera (77):

77 ÷ 2 = 38 resto 1
38 ÷ 2 = 19 resto 0
19 ÷ 2 = 9  resto 1
9 ÷ 2 = 4   resto 1
4 ÷ 2 = 2   resto 0
2 ÷ 2 = 1   resto 0
1 ÷ 2 = 0   resto 1

Resultado (leído de abajo arriba): 1001101

Parte decimal (0,1875):

0,1875 × 2 = 0,375  → 0
0,375 × 2 = 0,75    → 0
0,75 × 2 = 1,5      → 1
0,5 × 2 = 1,0       → 1

Resultado: 0,0011

Completo: 77,1875 = 1001101,0011 = 1001101,0011₂

Ejemplo 2: Binario a Decimal

1001101,0011₂ = 1×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 1×2² + 0×2¹ + 1×2⁰ + 0×2⁻¹ + 0×2⁻² + 1×2⁻³ + 1×2⁻⁴ = 64 + 0 + 0 + 8 + 4 + 0 + 1 + 0 + 0 + 0,125 + 0,0625 = 77,1875₁₀

Ejemplo 3: Hexadecimal a Decimal

BABA₁₆ = B×16³ + A×16² + B×16¹ + A×16⁰ = 11×4096 + 10×256 + 11×16 + 10×1 = 45090 + 2560 + 176 + 10 = 47836₁₀

Ejemplo 4: Octal a Decimal

423₈ = 4×8² + 2×8¹ + 3×8⁰ = 4×64 + 2×8 + 3×1 = 256 + 16 + 3 = 275₁₀

Conversión entre sistemas sin pasar por decimal

Binario a Octal

Agrupar los bits de 3 en 3 (desde la derecha)

(1 011 101)₂ = (135)₈

Binario a Hexadecimal

Agrupar los bits de 4 en 4 (desde la derecha)

(1010 1101 1010 0101)₂ = (ADA5)₁₆

Octal a Binario

Sustituir cada dígito por su valor en binario (3 bits)

(723)₈ = (111 010 011)₂

Hexadecimal a Binario

Sustituir cada dígito por su valor en binario (4 bits)

(A5B)₁₆ = (1010 0101 1011)₂

Fórmula general para conversión a decimal

Para un número en base B con dígitos d₁, d₂, …, dₙ: Decimal = d₁×B^(n-1) + d₂×B^(n-2) + … + dₙ×B^0

Aplicaciones de los distintos sistemas

• Binario: Fundamento de la electrónica digital y computación
• Octal: Utilizado históricamente para simplificar representaciones binarias
• Hexadecimal: Códigos de color web, direcciones de memoria, programación de bajo nivel
• Decimal: Uso cotidiano en matemáticas y comercio

Binario a Octal

Para convertir de binario a octal:

1. Agrupar los bits de 3 en 3 desde la derecha
2. Convertir cada grupo a su equivalente en octal

Ejemplo:

Binario: 5721 (101 111 010 001)
Agrupamos: (101) (111) (010) (001)
Equivalentes en octal: 5 7 2 1

Por tanto, 101111010001 en binario = 5721 en octal

Binario a Hexadecimal

Para convertir de binario a hexadecimal:

1. Agrupar los bits de 4 en 4 desde la derecha
2. Convertir cada grupo a su equivalente en hexadecimal

Ejemplo:

Binario: A51B (1010 0101 0001 1011)
Agrupamos: (1010) (0101) (0001) (1011)
Equivalentes en hexadecimal: A 5 1 B

Conversiones rápidas

Entre binario, octal y hexadecimal

La raíz común de estos sistemas facilita las conversiones:

• Base 2 (binario) es la raíz
• Base 8 (octal) = 2³
• Base 16 (hexadecimal) = 2⁴

Esto permite conversiones directas mediante tablas de equivalencia.

Conclusión

Dominar estos sistemas de numeración y sus conversiones es fundamental para comprender cómo funcionan los ordenadores a nivel básico. El sistema binario es la base de toda la informática moderna, mientras que el hexadecimal nos proporciona una forma compacta de representar valores binarios.

La práctica es fundamental para adquirir soltura con estas conversiones. Te animo a realizar ejercicios adicionales y utilizar la guía visual que he elaborado como referencia.